wher 101&#EJunger Modulus,-Idiametral Trägheitsmoment des Wellenabschnitts,-k initmh Kombi8211; Koeffizient der Momentsteifigkeit einer äquivalenten Verbindung, die dem vollständig offenen Riss entspricht. Die Gleichung hat zwei summands „ Kombium“; Flexibilität im Zusammenhang mit Riss und Flexibilität des Strahls ohne Riss.Es

 Es ist darauf hinzuweisen, dass unabhängig von der Strahlform, den Randbedingungen und der Rissposition, Beitrag zur allgemeinen Strahlflexibilität hängt nur vom Koeffizienten ab k initmh ,d.h. der erste Summand. Während der Strahl sich dreht, ändert sich die Flexibilität im Riss-Bereich.Wir erhalten folgende Informationen:wher 101 

 g o&#Flexibilität des Strahls ohne Riss,  q)=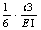 -kmhaktueller Koeffizient der momentanen Steifigkeit für die gegebeneqNein. -Integration von zwei Gleichungen (5) und (7), erhalten wir:wher101unter Berücksichtigung der Gleichung (6) erhalten wir das Gesetz der Veränderung der Momentsteifigkeit abhängig von der Differenz in phas

 es q 

 :Die erhaltene Momentsteifigkeit eines äquivalenten Verbindungs hängt nur von dem Wellendurchmesser, den Materialeigenschaften und der Risstiefe ab.Änderung der Rissposition in der Welle, die Eigenschaften der Welle einschließlich der Stützeinheiten ändern die Standfestigkeit einer gleichwertigen Verbindung nicht (auf&#unter der Bedingung, dass der Abschnitt mit Rissen in jedem Teil des Abschnitts mit Rissen, für die eserhalten).In der zuvor gewonnenen Steifigkeitsmatrix können die Steifigkeitskoeffizienten wie folgt geschrieben werden: wher 

101 k

init 

 e , k  init 

 hh Anfangswerte der Momentsteifigkeit an den entsprechenden Achsen für den vollständig offenen Riss&#Nein. Die Aufgabe der kinit e,kinit  -hhBerechnung kann auf zwei Arten gelöst werden.Die erste ist die Berechnung der Momentsteifigkeit im FEM-Programm.Die zweite ist die Theorie der Bruchmechanik zu verwenden.Es gibt die Möglichkeit, die Werte der Koeffizienten der lokalen Flexibilität des offenen Risses zu berechnen, wenn seine Geometrie, der Wellendurchmesser und die Materialeigenschaften bekannt sind [7,10].

 Algorithmus zur Simulation von Rotorsystem mit Rissen Die folgenden Schritte sollten durchgeführt werden, um Koeffizienten der Momentsteifigkeit des Risses zu erhalten.1. Das komplette Rotormodell wird in einem der spezialisierten Programme zur Analyse der Rotordynamik erstellt (fürBeispiel, in Dynamics R4).2. Der Rotorbereich mit Riss wird hervorgehoben.  3. Durch Riss wird der Wellenabschnitt in zwei Teilsysteme unterteilt.Link beschrieben durch die Matrix der VariablenKoeffizienten der Steifigkeit(SEUFZT)K (q) 

 , 

j)]

von

Dimension 6x6 wird zwischen Teilsystemen platziert.

4. Anfangskoeffizienten der Momentsteifigkeit

k

init

e ,kinithhbei offenen Rissen durch die angegebenen Methoden gewonnen werdenoben.Diese Daten sind initial für die Berechnung.Bei der Integration von Bewegungsgleichungen werden die Festigkeits-Matrix-Koeffizienten der Verbindung berechnet, die Rissbildung simulieren. 

des Rotorsystems für jedeqNein.Bei der nichtlinearen Deklarationsmatrix-Gleichung, die das nichtlineare dynamische Modell beschreibtdes Rotorsystems ist wie folgt: wher101(SEUFZT)M (SEUFZT)

Flächen 8211; Matrix der Trägheitskoeffizienten;

 (SEUFZT) C (SEUFZT)

Flächen 8211; Matrix der Dämpfungs- und Gyroskopkoeffizienten;(SEUFZT)K

(SEUFZT) 

 Matrix von Koeffizienten der Steifigkeit; *&#o*,*o*,*o*die Säulen der Schwingungsdrehungen, der Schwingungsgeschwindigkeiten und der Schwingungsbewegungen entsprechend;*-F(Beifall)t)*&&alle Arten von dynamischen Lasten im Bereich der Kombi- und Kombi-2-Ebene; intern und extern.Die Steifigkeitsmatrix eines äquivalenten Links kann in zwei Teile unterteilt werden: konstant und variabel, und folgendes ist wahr:(SEUFZT)&K Cist in die allgemeine Steifigkeitsmatrix des(SEUFZT)K(SEUFZT)System.Matrix() [q j] n,Kwird zur Berechnung verwendetReaktionen einer nichtlinearen Verbindung:-wher101 

 o rx , 

 o Arin units (real)Drehungen der Abschnitte um die entsprechenden Achsen.Die endgültige Bewegungsgleichung des Systems ist die folgende::Die angegebene Gleichung kann durch numerische Methoden wie Runge gelöst werdenKutta-Methode, Newmark-Methode, etc.Angemessenheit des vorgeschlagenen Algorithmus wird durch Vergleich der Flexibilität der beidenTrägerträger mitRiss im FiniteElementsystem und gemäß dem vermeintlichen Algorithmus in Dynamics R4.Die Aufgabe besteht darin, die Durchbiegung des Strahls unter der Einheit Kraft in den Rissabschnitten für verschiedene Phasen zwischen Riss und Kraft zu berechnen.Abbildung 3 zeigt die Ergebnisse der Überprüfung des vorgeschlagenen Algorithmus.Drei Ergebnisse werden verglichen:Flexibilität wird mit der Finite-Elemente-Methode (FEM) berechnet.Die Strahlflexibilität des Strahlmodells mit Rissen wird im FEM berechnet

System für den gesamten Bereich der Winkelstellung von Rissen;&#Flexibilität wird mit Dynamics R4 berechnet, erste Daten werden mit FEM ermittelt.Anfangswerte des MomentsSteifigkeit für den vollständig offenen Rissk inite, kinit

hhwerden gelöst Gleichung (7) für

k-init

mh-und radiale Flexibilität des Strahls mit Riss

gc-in der entsprechenden Richtung wird mit FEM berechnet.Die momentane Steifigkeit der mittleren Winkelstellung ändert sich nach dem (10) Gesetz von Minimum auf Maximum;

Flexibilität wird mit Dynamics R4 berechnet.Erste Daten der Zeitflexibilität für vollständig offene Risse

-k-e

 init , k-hh  

initwerden analytisch anhand der Algorithmen der Bruchmechanik [7, 10] gewonnen.Flexibilität für den Wert des MomentsZwischenkantige Risspositionen ändern sich nach dem Gesetz von Minimum auf Maximum (10).Abbildung 3 Veränderung der Strahlflexibilität im Crack-Sektor je Revolution Die Ergebnisse bei der Berechnung von FEMModell und Modelle in Dynamics R4 sind nah.Die Berechnungsergebnisse mit den ermittelten Ausgangsbedingungen unterscheiden sich analytisch von den FEM-Ergebnissen weniger als 1%.Gleichzeitig wird die ursprüngliche Steifigkeit analytisch viel schneller berechnet als die FEM-Berechnung und erfordert weniger Arbeitsstunden und so leichterzuverwenden.  Geometrie und Parameter des Rotors mit Riss Die Geometrie des Rotors mit Riss wird gewählt, um den Algorithmus am besten zu zeigen, Tabelle 1.Rotor mit der Zentralscheibe, die Stützen werden an den Wellenenden platziert.② ②②②

 ② ②-②②②②②②②②②  ② 

②

 ② ② ②-②-②-② 

②

 ② ② ②